
ヒストグラムを作っているんだけど、
棒の数とか幅をどうすればいいのか…?
こんな悩みを解決していきます。
この記事では、
ヒストグラムの棒の数を求める公式
を4つ紹介していきます。
その”4つ”はこちらになります。


え!文字がいっぱいで分からないよ…
という人も大丈夫です。文字ではなく日本語で置き換えたものも用意していますよ。
【はじめに】少なすぎ/多すぎはNG

棒の数なんて、適当でいいんじゃない?
と思っている人は、棒の数を適切に決めることの大切さをまずは知りましょう。
少なすぎると…
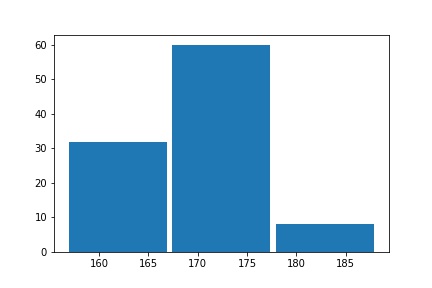
こちらのヒストグラムは、身長の分布を表したものです。
棒の数を3本にすると、分布の様子がよくわかりませんよね…。
おおざっぱな傾向は把握できますが、これだけでは詳しい分析ができません。
多すぎると…
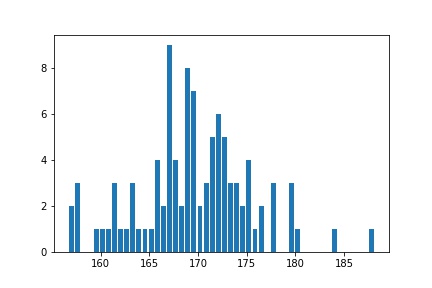
棒の数が少ないとダメなことがわかったので、棒の数を思いっきり増やしてみました。
しかしところどころデコボコになっていて、逆にわかりにくいです。
【本題】この4つの公式を使おう
では、棒の数を少なすぎず多すぎずにするためにはどうすればいいのでしょうか?
ヒストグラムの棒の数を適切に定めるのに役立つ、次の4つの公式を使ってみましょう。
・スタージェスの公式
・データ数の平方根
・スコットの選択
・FD選択
では、1つずつ解説していきます。
スタージェスの公式
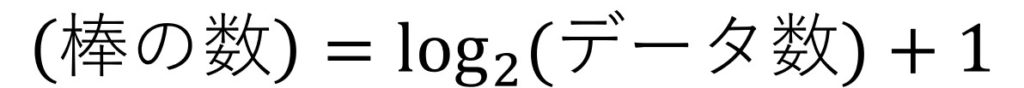
まずは、もっとも有名なスタージェスの公式です。先ほど【はじめに】で挙げた身長のデータを例に計算してみましょう。
上の身長データでは、
データ数 = 100
だったので、
棒の数= log2100 + 1 ≒ 7.6
となります。
よって、棒の数は7-8本くらいがちょうどいいという結論になります。
データ数の平方根
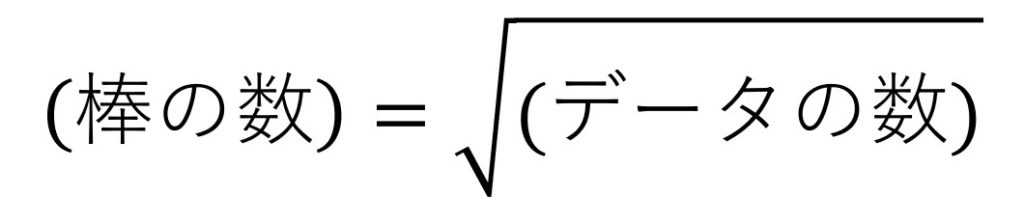
この公式はとても単純です。
単純にデータ数の平方根をとればOKです。
先ほどの身長データでいうと棒の数は,100の平方根なので「10本」となります。
スコットの選択
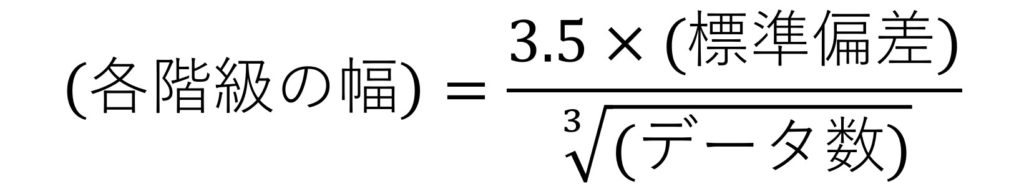
これはかなりマニアックな公式かもしれません。これも実際に計算してみましょう。
では、例として【はじめに】で挙げた身長データで計算してみましょう。
標準偏差 ≒ 5.847319
データ数 = 100
最大値 = 188.11
最小値 = 156.70
なので、
各階級の幅 = 3.5×5.847319 ÷ ∛100 ≒ 4.409183
ここで注意しなければいけないポイントが1つあります。
この公式では、階級の幅を求めていることに注意してください。
下の換算式を使えば「階級の幅」から「棒の数」に換算することができます。

これを使うと、
棒の数= (188.11-156.70)÷ 4.409183 ≒ 7.1
ということになります。
FD選択

これもなかなかマニアックな公式です。
*2つの式を書きましたが、
(四分位範囲)=(第3四分位数)-(第1四分位数)
と変形しただけのことです。
それでは、この公式でも計算してみましょう。
ここでも【はじめに】で挙げた身長データを使います。
第3四分位数 = 172.90
第1四分位数 = 166.6975
データ数 = 100
最大値 = 188.11
最小値 = 156.70
なので
階級の幅 = 2×(172.90 ー 166.6975) ÷ ∛100 ≒ 2.672576
となります。
ここで注意しなければならないことが1つあります。
この公式は「スコットの選択」と同様、階級の幅を求めるものです。
「スコットの選択」のところでも挙げた、下の換算式を使いましょう。

そうすると、
棒の数 = (188.11-156.70)÷ 2.672576 ≒ 11.8
となりました。
【まとめ】求めた「棒の数」をまとめてみた
これら4つの結果を表にまとめてみると、こんな感じです。
| 棒の数 | |
| スタージェスの公式 | 7.6 |
| 平方根 | 10 |
| スコットの選択 | 7.1 |
| FD選択 | 11.8 |
| 平均値 | 9.1 |
平均をとると、9本ぐらいだとわかったので、この本数でグラフを描いてみました。
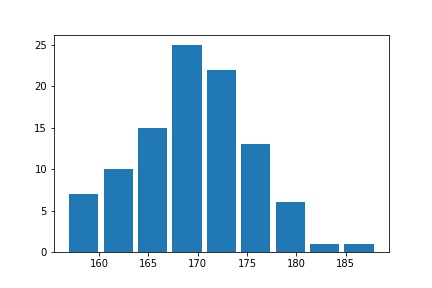
どうでしょう?わかりやすくないでしょうか。
最後に公式の復習をして終わりたいと思います。

というわけで、以上です。
最後まで読んでいただきありがとうございました。








記事への意見・感想はコチラ