今回の記事では、

さあ、このことを証明してみてください!
…と言われても「う~ん」と思わずうなってしまうような「あたりまえ過ぎて意外と証明が書けない」高校数学の証明問題を5つ紹介します。
問題
まずは問題を出すので、自分でどれくらい証明が書けるか試してみてください。
任意の集合A,Bに対して,\(\overline{A \cup B} = \overline{A} \cap \overline{B}\)が成り立つ。
集合が等しい(\(X=Y\))ということは,\(x \in X \iff x \in Y\)が成り立つことと同値です。
\(\overrightarrow{0}\)でない2つのベクトル\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が互いに平行でないとき,次が成り立つ。
$$s\overrightarrow{a}+t\overrightarrow{b}=u\overrightarrow{a}+v\overrightarrow{b}\iff s=u,t=v$$
背理法で示してみましょう。
\(r>1\)のとき,\(\displaystyle \lim_{n \to \infty}r^n=\infty\)
任意の正の数 h をとると、r=1+h は r>1 を満たします。
区間\(I\)内の任意の\(x\)で\(f'(x)>0\)ならば, 区間\(I\)で \(f(x)\)は単調に増加する。
平均値の定理を使います。
曲線 \(y=f(x)\)と直線 \(x=a, x=b, y=0\) (\(a<b\)) で囲まれた領域の面積は\(\displaystyle S=\int_{a}^{b}f(x)dx\)である。ただし \(f(x)\)は任意の \(x \in [a,b]\)で正かつ連続な関数とする。
微小幅の面積を、長方形の面積で評価してみましょう。
解説
【数Ⅰ】ド・モルガンの法則
任意の集合A,Bに対して,\(\overline{A \cup B} = \overline{A} \cap \overline{B}\)が成り立つ。
(証明)
\(x \in \overline{A \cup B} \iff x \in \overline{A} \cap \overline{B}\)を示せばよい.
$$\begin{align*}
x \in \overline{A \cup B} &\iff x \notin A \cup B \\
&\iff x\notin A かつ x\notin B \\
&\iff x \in \overline{A} かつ x \in \overline{B} \\
&\iff x \in \overline{A} \cap \overline{B}
\end{align*}$$
よって \(\overline{A \cup B} = \overline{A} \cap \overline{B}\)
集合X,Yが\(X=Y\)となるとき,Xの要素(元)は必ずYの要素であり,その逆もまた然りです。したがって\(X=Y\)が成り立つことと\(x \in X \iff x \in Y\)が成り立つことは同値です。
それを踏まえれば、あとは言い換えを行っていけばよいです。
1行目は補集合の定義そのものです。
1行目は「xはAとBの和集合に入ってない」と言っているのでそれは「xはAにもBにも入ってない」ことと同じことです。よって2行目がしたがいます。
2-3行目の言い換えも補集合の定義です。
3-4行目は共通部分の定義です。
ちなみに、もう1つのド・モルガンの法則「\(\overline{A \cap B}=\overline{A} \cup \overline{B}\)」は、\(A’=\overline{A},B’=\overline{B’}\)とおいて、両辺の補集合をとると導けます。
\(A’=\overline{A},B’=\overline{B’}\)とおくと、 \(\overline{A \cup B} = \overline{A} \cap \overline{B}\) より
$$\begin{align*}
\overline{\overline{A’} \cup \overline{B’}} = A’ \cap B’\\
\therefore \overline{\overline{\overline{A’} \cup \overline{B’}}}=\overline{A’ \cap B’}\\
\therefore \overline{A’} \cup \overline{B’}=\overline{A’ \cap B’}\\
\end{align*}$$
【数B】1次独立と係数比較
\(\overrightarrow{0}\)でない2つのベクトル\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が互いに平行でないとき,次が成り立つ。
$$s\overrightarrow{a}+t\overrightarrow{b}=u\overrightarrow{a}+v\overrightarrow{b}\iff s=u,t=v$$
(証明)
【 ⇐ の証明】
代入すれば(左辺)=(右辺)は明らか.
【 ⇒ の証明】
\(s \neq u\)と仮定すると,
$$\begin{align*}
s\overrightarrow{a}+t\overrightarrow{b}=u\overrightarrow{a}+v\overrightarrow{b}&\iff (s-u)\overrightarrow{a}=(v-t)\overrightarrow{b}\\
&\iff \overrightarrow{a}=\frac{v-t}{s-u}\overrightarrow{b}
\end{align*}$$
となるがこれは,\(v \neq t\)のときは「2つのベクトル\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が互いに平行でない」という条件に反し.\(v = t\)のときは「\(\overrightarrow{a} \ne \overrightarrow{0}\)」という条件に反する. よって \(s = u\)がわかる.
同様に\(t \neq v\)と仮定すると,背理法により\(t=v\)がわかる.
よって\( s\overrightarrow{a}+t\overrightarrow{b}=u\overrightarrow{a}+v\overrightarrow{b}\implies s=u,t=v\)
この証明のように、\(s-u\)がゼロでないと仮定し、両辺を\(s-u\)で割って矛盾を導くというやり方はよくします。
\(s=u\)が導けた後は、「同様に…」として\(t=v\)を示しても良いですし、\(s=u\)を\(s\overrightarrow{a}+t\overrightarrow{b}=u\overrightarrow{a}+v\overrightarrow{b}\)に適用することで\(t=v\)を示してもOKです。
【数Ⅲ】数列の極限
\(r>1\)のとき,\(\displaystyle \lim_{n \to \infty}r^n=\infty\)
(証明)
任意に正の数\(h\)をとり,\(r=1+h\)とすると\(r>1\)となる.
二項定理から,十分大きな自然数n≧2に対して
$$\begin{align*}
r^n &= (1+h)^n\\
&= {}_nC_0 + {}_nC_1 h + {}_nC_2 h^2 + \cdots + {}_nC_n h^n\\
&= 1 + nh + \frac{n(n-1)}{2} h^2 + \cdots + h^n\\
&> 1 + nh
\end{align*}$$
となる.いま\(h>0\)より\(\displaystyle \lim_{n \to \infty}(1+nh)=\infty\)だから,追い出しの原理により\(\displaystyle \lim_{n \to \infty}r^n = \infty\)
r=1+h とおくのは少しトリッキーかもしれませんね。高校段階ではこういうおき方はなかなかしないかもしれません。
しかし、r=1+h とおいた後の流れは数Ⅲで習う「近似」でも出てきた考え方ですので、サッと出てくるようにしておくのが望ましいと思います。
任意のK>0に対し,\(N=\log_{r}K\)とおけば(r>1より\(N<\infty\)),
$$n>N \implies r^n>r^N=r^{\log_{r}K}=K$$
となる.よって発散の定義から\( \displaystyle \lim_{n \to \infty}r^n = \infty \)
【数Ⅱ(数Ⅲ)】導関数と単調性
区間\(I\)内の任意の\(x\)で\(f'(x)>0\)ならば, 区間\(I\)で \(f(x)\)は単調に増加する。
(証明)
任意に\(\alpha,\beta\in I\ (\alpha<\beta)\)をとると,平均値の定理から
$$f(\beta)-f(\alpha)=(\beta-\alpha)f'(c)$$
となる実数 \(c\ (\alpha<c<\beta)\) が存在する.
仮定から,\(f'(c)>0,\ \beta-\alpha>0\)なので右辺は正となる.したがって \(f(\beta)>f(\alpha)\) となるから,\(f(x)\)は区間\(I\)内で単調に増加する.
区間Iでf(x)が単調に増加することの定義は、\(\alpha,\beta\in I\)に対し,
$$\alpha < \beta \implies f(\alpha) < f(\beta)$$
が成り立つことです。つまり,\(f(\beta)-f(\alpha)>0\)が示せればいいわけです。
「同じ関数の差が出てきたら平均値定理の利用を考える」は定石ですから、定義が頭に浮かびさえすれば証明は難しくないはず。
【数Ⅱ(数Ⅲ)】積分は面積
曲線 \(y=f(x)\)と直線 \(x=a, x=b, y=0\) (\(a<b\))で囲まれた領域の面積は\(\displaystyle S=\int_{a}^{b}f(x)dx\)である。ただし \(f(x)\)は任意の \(x \in [a,b]\)で正かつ連続な関数とする。
注意:「微小幅\(dx\)の長方形を\(x=a\)から\(x=b\)まで集めたものだから…」 というのは直感的な説明にすぎず、証明になっていません。
(証明)
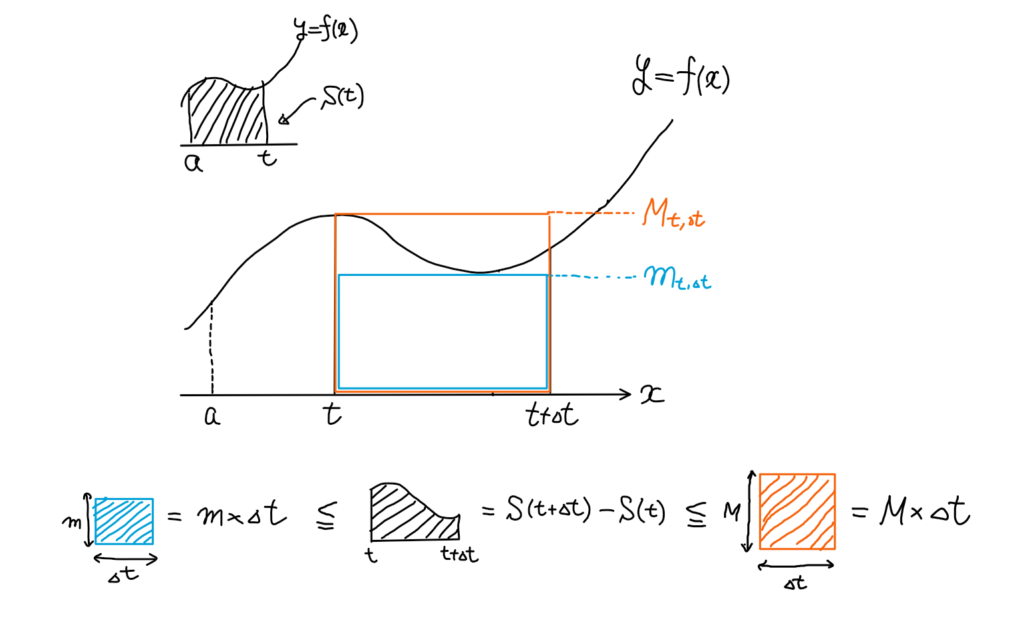
曲線 \(y = f(x)\) と直線 \(x = a, x = t, y = 0\) で囲まれる面積を \(S(t)(a ≦ t ≦ b)\) とする.また\(\Delta t > 0\) に対して,区間\( [t, t + ∆t] \)における \(f(x)\) の最大値および最小値は存在し,それぞれ \(M_{t,\Delta t}, m _{t,\Delta t} \)とおく.このとき
$$\begin{align*}
m _{t,\Delta t} \Delta t \leq S(t + \Delta t) − S(t) \leq M _{t,\Delta t} \Delta t \\
\therefore m _{t,\Delta t} \leq \frac{S(t + \Delta t) − S(t)}{\Delta t} \leq M _{t,\Delta t}
\end{align*}$$
\(\Delta t < 0\)のときも同様にして
$$ m _{t,\Delta t} \leq \frac{S(t) – S(t + \Delta t)}{\Delta t} \leq M _{t,\Delta t} $$
となる.ここで\(\displaystyle \lim_{\Delta t \to \pm 0}M _{t,\Delta t} = \lim_{\Delta t \to \pm 0}m _{t,\Delta t} = f(t) \)に注意すると、はさみうちの原理により
$$\begin{align*}
\lim_{t \to +0} \frac{S(t + \Delta t) − S(t)}{\Delta t} &= \lim_{t \to -0} \frac{S(t) – S(t + \Delta t)}{\Delta t} = f(t)\\
\therefore \lim_{t \to 0} \frac{S(t + \Delta t) − S(t)}{\Delta t} &= f(t)\\
\therefore S'(t)&=f(t)
\end{align*}$$
となる.ここで\(f(t)\)の原始関数をF(t)とすれば,
$$S(t)=F(t)+C\ (Cは積分定数)$$
この式で\(t=a\)および\(t=b\)とすると
$$\left\{\begin{array}{}
0=F(a)+C\\
S=F(b)+C
\end{array}\right.$$
これら2式の辺々引いて
$$\begin{align*}
S=F(b)-F(a)\\
\therefore S=\int_{a}^{b}f(x)dx
\end{align*}$$
これをきちんと証明できた人は数Ⅲの力がしっかりついていると言えます。
証明のポイントは「長方形の面積でSを不等式評価する」です。区間内のf(x)の最大値最小値を用いて評価することができます。
すると真ん中に\(S(t+\Delta t)-S(t)\)という見覚えのある式が出てくるので、あとは導関数の定義に持ち込んでいくという流れです。
最後は積分記号\(\int\)の定義を使って締めてください。
※万が一、問題・解答解説に不備がありましたら、ページ下部のコメント欄か,お問い合わせまたはTwitterで報告してください。






記事への意見・感想はコチラ