
高校の数学で「条件つき確率」を習ったけど、アレ意味あるのかな?
この記事を読むと、
- ふつうの確率とは何が違うのか?
- 条件つき確率はどこで使えるのか?
が分かるようになっています。ぜひ最後までご覧ください。
条件付き確率とは
条件つき確率とは、Wikipediaの表現を借りると
条件付き確率は、ある事象 B が起こるという条件下での別の事象 A の確率のことをいう。条件付き確率は P(A|B) または PB(A) のように表される。条件付き確率 P(A|B) はしばしば「B が起こったときの A の(条件付き)確率」「条件 B の下での A の確率」などと表現される。
「条件付き確率」Wikipedia,2020年11月16日 (月) 09:56 最終更新,https://ja.wikipedia.org/wiki/条件付き確率
となります。
つまり条件付き確率とは、「事象Bが起こったのが事実であるとき、事象Aが起こるのはどれくらいの確率なの?」ということを表したものと言えます。
簡単な図に表すと下のような感じです。
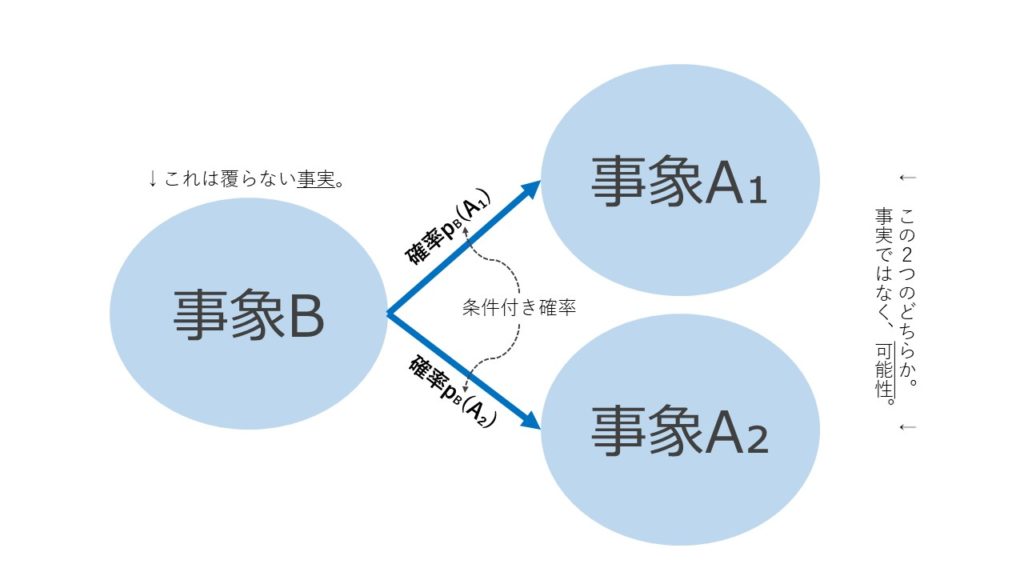
「B」という覆しようのない事実があって、そのときに「A₁となる確率」「A₂となる確率」を求めたら、それは「Bという条件のもとでの条件付き確率」であると言えます。
ふつうの確率との違い

ふつうに「確率」って言う場合と何がちがうの?
と疑問に思う人がいるかもしれませんが、別に難しくはありません。
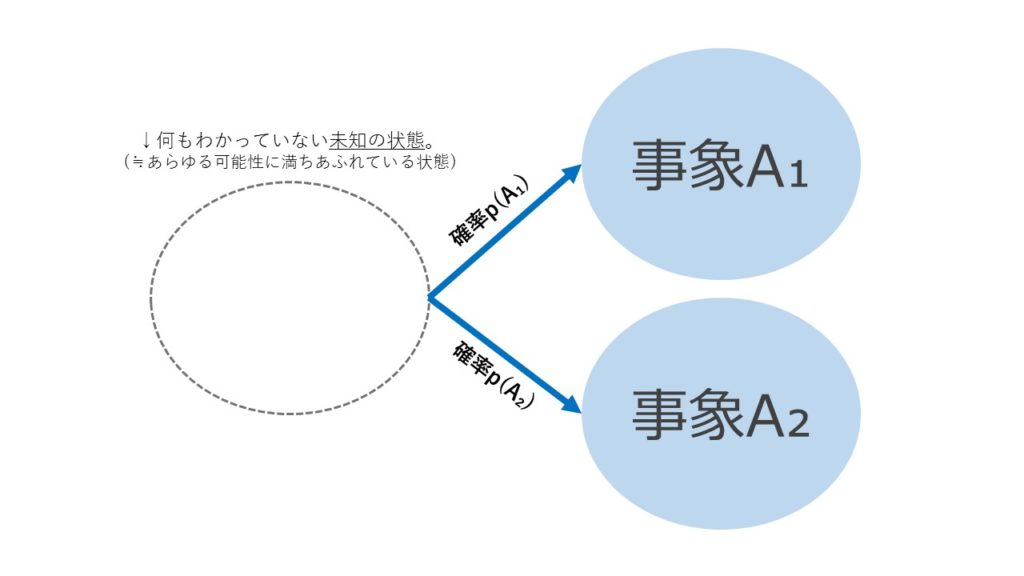
普通の確率は、単に「”条件付き”ではない確率」ということですから、さっきの例で言うと「事象B」という事実がない(未確定)状態を考えたときの確率です。
なので、さっきの図と同じように書くと下のようになります。
条件つき確率が役立つ2つの事例
さてここからが本題です。
条件つき確率の考え方が活躍する以下の2つのケースについて考えていきましょう。
- DNA鑑定で一致=真犯人?
- PCR検査の”精度”とは?
DNA鑑定で一致!でも本当に犯人?
DNA鑑定は、犯罪事件の捜査に使われることがあります。
DNA鑑定の精度は、現在では約4兆7000億人に1人しか一致しない*¹ほどと言われています。
しかし昔のDNA鑑定は精度が悪く、鑑定結果を過信した結果誤認逮捕されてしまった方もいます。その事件の一つが「足利事件」です。
事件当時のDNA鑑定の精度は1000人に1人ほどであったと言われています。百分率にすると0.1%です。
言い換えれば99.9%の精度で鑑定できるのだから、一致すれば「こいつが犯人だ!」と思うのが自然かもしれません。しかしよくよく考えたら全くそうではないことがわかります。
ポイントは「割合でみると小さいが、絶対的な量でみると小さくはない」ことです。
例えば、事件当時の足利市の人口は約17万人ですが、全員にDNA鑑定を行えばおよそ170人の鑑定が一致してしまう計算になります。これでは意味がありません。
この170人の中から1人の真犯人を見つけなければならないのですから、DNA鑑定が一致してもその人が真犯人とは限りません。
では以上のことを、表を使いながら条件つき確率で考えてみましょう。次の表を使います。
| DNA鑑定一致 | DNA鑑定不一致 | |
| 有罪 | ||
| 無罪 |
まず前提として、DNA鑑定を行った対象の中に真犯人がいるとしましょう。もしかすると鑑定対象に真犯人がいない可能性もありますが、今回はその場合は考えないことにします。
そうすると表は次のようになりますね。
| DNA鑑定一致 | DNA鑑定不一致 | |
| 真犯人 | 1人 | 0人 |
| 無実 |
次に、DNA鑑定の精度を「1000人に1人一致」として、DNA鑑定を足利市(人口17万人)全員に行ったとしましょう。すると、
無実で、かつDNA鑑定不一致=169,830人
無実なのに、DNA鑑定一致=170人
ですから、表はこうなります。
| DNA鑑定一致 | DNA鑑定不一致 | |
| 真犯人 | 1人 | 0人 |
| 無実 | 170人 | 169,830人 |
この表を使って、検察側の誤りを検証しましょう。
検察側は、

1000人に1人しか一致しないのだから、一致したらその人が真犯人に決まっている!
と主張します。この主張を表で見ると、
| DNA鑑定一致 | DNA鑑定不一致 | |
| 真犯人 | 1人 | 0人 |
| 無実 | 170人 | 169,830人 |
と、横方向に見ていることがわかります。しかしこの見方は、この場合ではおかしいです。
「無実であることを前提としたとき、DNA鑑定が一致する条件つき確率は 0.1%」
という見方をしているようですが、鑑定が一致したかしていないかはもうすでに確定している事実なので、一致するかどうかの確率を求める意味がないわけです。
つまり、条件つき確率の「条件」の設定を誤ってしまっているのです。
一方弁護側は

DNA鑑定が一致している場合に、その人が無実である確率は 169/170≒94.4% もある!
と主張します。この主張を表で見ると、
| DNA鑑定一致 | DNA鑑定不一致 | |
| 真犯人 | 1人 | 0人 |
| 無実 | 170人 | 169,830人 |
と、縦方向に見ていることがわかります。
「DNA鑑定が一致していることを前提としたとき、無実である条件つき確率は 約94.4%」
としていますが、これは適切な条件が設定されています。DNA鑑定の結果はすでにわかっているのだから、それを前提として真犯人かどうかを確かめるべきなのです。
PCR検査で陽性!でも本当に感染してる?
2020年から世界的に流行したCOVID-19ですが、感染したかどうかをPCR検査で判定する場合が多いですよね。
しかしPCR検査の精度は絶対ではなく、その精度は約70%と言われます。しかしこの言い方は正確ではありません。精度といってもいろいろな見方ができます。
これも表を使って考えてみましょう。
まず一つの見方として、精度を「感染している人が、陽性となる率」とするものです。
これは「検査の感度」「真陽性率」とも言われ、先ほどの70%という数字はこのことを指しています。
これを表に書き込むとこうなります。
| 陽性 | 陰性 | (計) | |
| 感染 | 70人 | 30人 | (100人) |
| 非感染 | (9,900人) |
もう一つの見方として「感染していない人が、陰性となる率」を精度とみなす考えもアリですよね。
これは「特異度」「真陰性率」とも言われ、PCR検査は約99.9%と言われています。
このことも表に書き込んでおきましょう。
| 陽性 | 陰性 | (計) | |
| 感染 | 70人 | 30人 | (100人) |
| 非感染 | 10人 | 8,890人 | (9,900人) |
はい、これで表が完成しました。この表を使って条件付き確率を考えてみます。
例えば、

PCR検査で陽性でした。でも感染していない気が…?
こんな場合を条件付き確率で考えてみましょう。
| 陽性 | 陰性 | (計) | |
| 感染 | 70人 | 30人 | (100人) |
| 非感染 | 10人 | 8,890人 | (9,900人) |
陽性であることはわかっているのだから、表をタテにみて条件付き確率を考えなければなりません。
すると「陽性なのに、感染していない」確率は、10/80=12.25%となります。8人に1人と、割と多めな気がしますね。
逆パターンも同じように考えることができます。

PCR検査で陰性でした。でも家族は陽性だったし本当は感染しているんじゃ…?
という場合です。
| 陽性 | 陰性 | (計) | |
| 感染 | 70人 | 30人 | (100人) |
| 非感染 | 10人 | 8,890人 | (9,900人) |
すると「陰性なのに、感染している」確率は、30/8920 ≒ 0.3% となります。こちらは結構低めですね。
つまり、PCR検査は非感染者も感染者とみなされてしまう場合はやや多いけれど、感染者なのに検査でスルーされる確率は低いよー、ということがわかります。
まとめ
今回は、条件付き確率の考え方が実際どう役に立つかについて、具体例を通して解説しました。
具体例で見てきたように、2×2のクロス表を書きながら条件付き確率を考えるとわかりやすいので、頭が混乱する人はぜひ表を活用してみてください。
↓本記事を書くきっかけになった書籍(特にp.292~)。
*¹ この数字は実証に基づいてはじき出されたものではなく、複数のパターンの出現率を掛け合わせただけのもの。確率同士をかけ算する際には独立かどうかの確認が必要ですが、その検証は行われていないためこれはあくまで理論上の数値です。






記事への意見・感想はコチラ