学食のレシートの「1食の目安」を最適化

今回は、
学食の栄養バランスピタリ賞
となるメニューの組み合わせを探してみたらヤバすぎる組み合わせになったよ、って話をします!
上に貼った写真は、とある日に生協の食堂でもらったレシートです。
「1食の目安」という部分を見ると、男性の場合
赤:2.7点 緑:1.0点 黄:5.7点
が理想みたいですが、この日に選んだメニューでは
赤:4.9点(+1.2点超過) 緑:0.2点(-0.8点不足) 黄:7.5点(+1.8点超過)
となっておりました。
ミールカードが使える日は毎日食べているのですが、なかなか理想の点数にはたどり着けません。そこで、どういう組み合わせなら理想の点数になるのか?と気になったんです。
プログラム書いてピタリ賞を見つける
ということでプログラムを書いて、ベストな学食メニューの選び方を探索します。
今回は次の3つの方法を試してみました。
- 総当たり法
全ての組み合わせを調べつくす - 変数固定法
最初は適当に選んで、誤差が小さくなるように修正する - 線形計画法
制約をみたすように、目的変数を最小化する組を求める
下へ行くにつれ、計算量が小さくなっています。
総当たり法:O(2ⁿ)
総当たり法では、ありうる全ての組み合わせを調べ上げ、ピタリ賞となるかどうかを判定します。
# 変数datには栄養点数の値が入っている
"""
例:
dat = np.array( [[1.8, 0.1, 3.3],
[2.2, 0.1, 0.3],
[1.4, 0.6, 1.7]] )
例えば、
dat[0][0]はメニュー番号=0 の品の「赤」の点数を表し、
dat[2][1]はメニュー番号=2 の品の「緑」の点数を表し、
dat[1][2]はメニュー番号=1 の品の「黄」の点数を表す。
"""
for i in itertools.product([0,1], repeat=len(dat)):
# 選んだ品をindex値へ変換してselectに格納
select = [k for k,v in enumerate(list(i)) if v==1]
# 栄養点数の合計を、赤・緑・黄のそれぞれについて合計(内積を使って計算)
total = np.dot(np.ones(len(select)), dat[select])
# 理想の点数との絶対値誤差をerrorに格納
error = abs(total[0]-2.7) + abs(total[1]-1.0) + abs(total[2]-5.7)
# errorが十分小さければ、そのメニューの組み合わせを出力
if error < 0.01: # 数値計算で誤差が生じるのでerror==0とはしていない
print(f"select numbers : {select}, absolute error : {error}")この方法が最もわかりやすいのですが、計算量がとてつもなくデカいです。
例えば、ある食堂のある日のメニューが全20品だとしましょう。
すると、全ての組み合わせは 220=1,048,576 ≒ 100万通りとなります。
100万通りなら、十数分くらい待てば調べ上げられますが、もし全30品となると全ての組み合わせは230=1,073,741,824 ≒ 10億通りとなります。
ここまでくるとかなり時間がかかります。
一般には、全n品からの選び方は 2ⁿ 通りあるので、nが大きくなると爆発的に増えます。
時間をかければ不可能ではないですが、ベストなメニューの組み合わせを知るというしょうもないことのためだけに長い時間待ちたくはありません。なのでもっと早く見つける方法を考えます。
変数固定法:O(n³)
そこで考え付いたアルゴリズムは、次のようなものです。
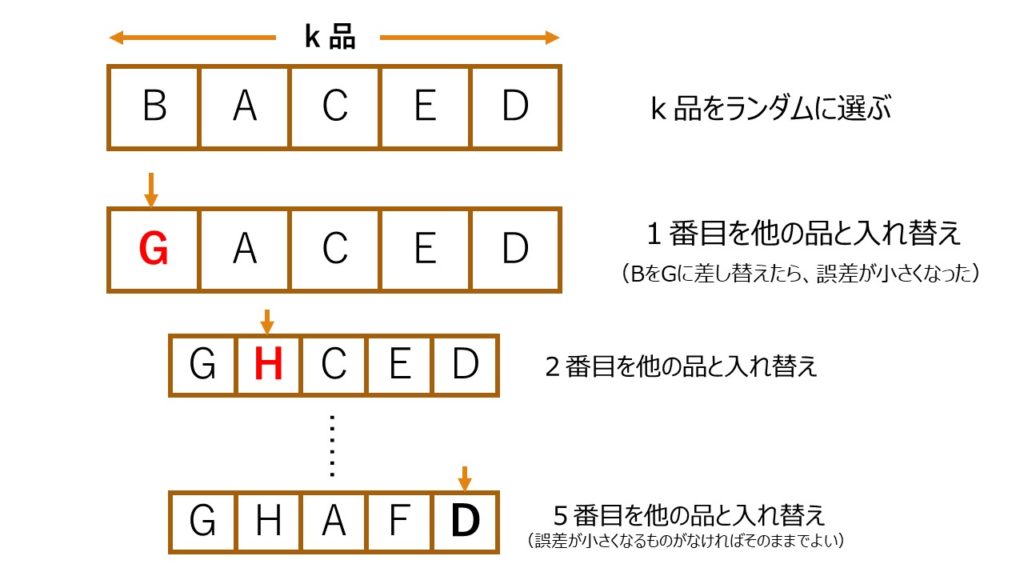
- 全n品 の中からk品 をランダムに選ぶ。(1≦k≦n)
- そのk品 のうちi番目の品を選ぶ。(1≦i≦k)
- そのi番目の品のみを他の品と入れ替えたときに、最も誤差が小さくなるものを探し、それをi番目の品と置き換える。
- 以上の操作をすべてのk,iについて繰り返す。
他の要素はすべて固定しておいて、1つだけ動かしていくので変数固定法という名前を付けました。
# 誤差を計算する関数
def calc_error(a):
return abs(a[0]-2.7) + abs(a[1]-1.0) + abs(a[2]-5.7)
# 選んだ品の合計を求める関数
def calc_sum(a):
return np.dot(np.ones(len(a)), a)
# 変数datには栄養点数の値・値段が入っている
"""
例:
dat = np.array( [[1.8, 0.1, 3.3, 308],
[2.2, 0.1, 0.3, 308],
[1.4, 0.6, 1.7, 264]] )
例えば、
dat[0][0]はメニュー番号=0 の品の「赤」の点数を表し、
dat[2][1]はメニュー番号=2 の品の「緑」の点数を表し、
dat[1][2]はメニュー番号=1 の品の「黄」の点数を表し、
dat[0][3]はメニュー番号=0 の品の値段を表す。
"""
# 選ぶ最大個数
k = len(dat)
# イテレーション数
iterations = 1
for n in range(1,k+1):
print("="*10, f"select{n}", "="*10)
# 初期点を設定する
select = random.sample(range(len(dat)), n)
not_select = [i for i in range(len(dat)) if i not in select]
P = dat[select]
# 初期点での誤差を計算する
e = calc_error(calc_sum(P)[:3])
print("e =",e)
# i番目の品のみを動かして、誤差を改善する
e_i = 1000
for iter_n in range(iterations):
print("-"*5, f"iteration{iter_n+1}", "-"*5)
for i in range(n):
select_tmp = select.copy()
not_select = [i for i in range(len(dat)) if i not in select]
for d,id_ in zip(dat[not_select], not_select):
tmp = P.copy() # Pの分身を作る
tmp[i] = d # i番目の品を新しいdに取り換える
if calc_error(calc_sum(tmp)[:3]) < e_i: # もし取替後に誤差が改善したならば
e_i = calc_error(calc_sum(tmp)[:3]) # 誤差e_iを更新し、
P = tmp # 点Pも更新する
select_tmp[i] = id_
select = select_tmp
print(f"e_{i+1} =",e_i) # i番目の品を色々動かした結果、誤差がどうなったか出力
print("-"*20)
print(f"total : {calc_sum(P)[:3]}")
print(f"price : {calc_sum(P)[-1]}円")
print(f"select {k} : {select}")
print("="*30,"\n")こうすると、計算量はだいたい
$$\sum_{k=1}^{n}\sum_{i=1}^{k}(n-1)=\frac{1}{2}n(n+1)(n-1)=O(n^3)$$
となります。nが1桁の場合は先ほどの総当たり法使った方が早いですが、今回の場合nは2桁なのでこちらの方が早く求まります。
実際n=20の場合、およそ3000回の入れ替え操作で済むので、総当たり(100万通り)に比べてかなり早いことがわかります。
しかし出てくる解は「できるだけ誤差が小さい」というだけで、最適解とは限りません。
初期点がうまいところに取れていないと、最適解にはなりません。
線形計画法
最後に、おそらく最も合理的なアルゴリズムであろう線形計画を使ってみました。
制約条件を次のように定め、Pythonの線形計画法ライブラリである「pulp」に投げました。
$$\begin{align*}
\left|\sum_{i=1}^{n}\text{Red}(i)x_i\ -\ 2.7\right| = 0\\
\left|\sum_{i=1}^{n}\text{Green}(i)x_i \ -\ 1\right| = 0\\
\left|\sum_{i=1}^{n}\text{Yellow}(i)x_i\ -\ 5.7\right| = 0\\
x_i \in \{0,1\}\ \ (i=1,2,\cdots,n)\\
\end{align*}$$
なお、\(\text{Red}(i)\)などは、i番目の品の「赤」の値を返す関数とします。
import pulp
# 変数datには栄養点数の値が入っている
"""
例:
dat = np.array( [[1.8, 0.1, 3.3],
[2.2, 0.1, 0.3],
[1.4, 0.6, 1.7]] )
例えば、
dat[0][0]はメニュー番号=0 の品の「赤」の点数を表し、
dat[2][1]はメニュー番号=2 の品の「緑」の点数を表し、
dat[1][2]はメニュー番号=1 の品の「黄」の点数を表す。
"""
red = dat.T[0]
green = dat.T[1]
yellow = dat.T[2]
problem = pulp.LpProblem("学食最適化", pulp.LpMinimize)
x = [pulp.LpVariable( f"x_{i}", cat=pulp.LpBinary) for i in range(len(dat))]
problem += pulp.lpDot(red, x) - 2.7 == 0
problem += pulp.lpDot(green, x) - 1.0 == 0
problem += pulp.lpDot(yellow, x) - 5.7 == 0
status = problem.solve()
print("Status:", pulp.LpStatus[status])
select = [i for i in range(len(x)) if pulp.value(x[i])==1]
total_price = np.dot(price, [x[i].value() for i in range(len(x))])
print(select)
print(f"price : {total_price}円")線形計画法には「シンプレクス法」といったアルゴリズムがあるそうなので、高速かつ最適な解を求めることができます。
「栄養点数ピタリ賞」のメニュー全5種
記事執筆時点での吉田食堂のメニューを参考にした、栄養点数ピタリ賞のメニューを全てご紹介します。





なんと…!ほとんど副菜とデザートのみっていうね…。主菜が入っているのは5枚目の画像だけです。
かなりの割合で「牛乳orコーヒー」「コロッケ」「サラダ」が入っているのもわかります。
こんなことになったのは、おそらく次のような理由からだと思います。
- 主菜や丼物を選ぶと、その1品だけで点数を超えてしまう
- 一方、小鉢のメニューは点数を調整しやすい
- そもそも「1食の目安」で示されている点数の決め方に違和感
(カロリーだけで点数が決まる)
時間があったら、
- 主食を必ずいれる、という制約条件をつける
- 栄養点数ではなく、カルシウムなど個々の栄養素を最適化する
みたいなこともやってみたいなーって思います。







記事への意見・感想はコチラ