実験の目的
機械学習における label encoding(ordinal encoding)とは、カテゴリ変数を数値に変換する手法の1つで、各水準を単純に整数に置き換えるものです。
例えば、「日本」「アメリカ」「イギリス」といったラベル(水準)をそれぞれ「0」「1」「2」と振り分けます。
| 変換前 | 変換後 |
|---|---|
| 日本 | 0 |
| アメリカ | 1 |
| イギリス | 2 |
| 日本 | 0 |
| アメリカ | 1 |
しかし数値の割り当て方には決まったルールはなく、好きなように変換を施すことができます。
| 変換前 | 変換後① | 変換後② |
|---|---|---|
| 日本 | 0 | 1 |
| アメリカ | 1 | 2 |
| イギリス | 2 | 0 |
| 日本 | 0 | 1 |
| アメリカ | 1 | 2 |
なので、整数の割り当て方によって精度が高くなったり低くなったりします。
そこで生じる疑問は、

どういう割り当て方をすれば、精度が上がるのか…?
という疑問です。
そんなわけで今回の実験では、label encodingの方法によって精度がどうなるのかを、後述する3つのモデル別に検証しました。
一般的によく言われていること
まず、label encodingに関する知見について調査しました。
”普通の” label encodingとは
特別な理由がなければ、label encodingは辞書順に並べた順のインデックスでencodeされるようです。[1]
| 変換前 | 変換後 |
|---|---|
| blue | 0 |
| green | 1 |
| red | 2 |
| yellow | 3 |
| green | 1 |
label encodingが適さない機械学習モデル
しかし、辞書順に基づいてencodingを行ってもその整数の順序には(ほとんどの場合)意味がありません。これは統計学の用語でいうと「名義尺度」で、水準間に大小関係はなく、同じかどうかという情報のみが意味を持ちます。
なので、例えば線形回帰モデル
$$\hat{y} = w_1x_\text{country} + \cdots$$
の場合、\(x_\text{country}\)の値によって予測値が変わりますが、日本(=0)、アメリカ(=1)、イギリス(=2)、…となるにつれて予測値が増大してしまいます。日本・アメリカ・イギリスの間に明確な大小関係は無いにもかかわらず、です。
このため、値の大きさに意味を持つモデルにlabel encodingはあまり適していません。
*ニューラルネットワークもこれに含まれそうですね。
しかし決定木系のアルゴリズムなら、label encodingは適しています。
決定木では、(かなりざっくり言うと)
・\(x_\text{country}\)が0なら、\(\hat{y}=100\)
・\(x_\text{country}\)が1なら、\(\hat{y}=150\)
・\(x_\text{country}\)が2なら、\(\hat{y}=90\)
…
というふうに、(うまく分岐がされれば)値の大小には影響されないモデルになります。そのため、決定木系のアルゴリズムではlabel encodingを直接使っても問題なさそうです。
実験の方法
Kaggleの常設コンペ「House Prices – Advanced Regression Techniques」のデータを用いて、実験を行いました。
次の4通りの label encoding (とone-hot encoding)を比較します。
- SklearnのLabelEncoderでエンコーディングした場合
- 目的変数の平均の昇順に0以上の整数を割り振った場合*
- 目的変数の中央値の昇順に0以上の整数を割り振った場合*
- ラベルの頻度の昇順に0以上の整数を割り振った場合
- (おまけ)one-hot encodingの場合
「目的変数の平均の昇順に0以上の整数を割り振る」とは、こういうことです。
| x(説明変数) | y(目的変数) |
|---|---|
| 緑 | 100 |
| 青 | 50 |
| 赤 | 90 |
| 青 | 80 |
| 赤 | 110 |
| 緑 | 160 |
| xのカテゴリ | yの平均 |
|---|---|
| 青 | 65 |
| 赤 | 100 |
| 緑 | 130 |
| x(変換前) | x(変換後) | y(目的変数) |
|---|---|---|
| 緑 | 2 | 100 |
| 青 | 0 | 50 |
| 赤 | 1 | 90 |
| 青 | 0 | 80 |
| 赤 | 1 | 110 |
| 緑 | 2 | 160 |
そして、モデルによる違いも検証するため、上記の各場合について
- 線形回帰
- ランダムフォレスト
- LightGBM
の3種類のモデルで比較しました。
線形回帰では欠損値が扱えません。したがって、元データから ①欠損値が大部分を占める列を削除し、②欠損値を1つ以上ふくむ行を削除しました。もちろん、この欠損値処理は3モデル共通です。
上記処理後のデータは1460行×20列で、このうち80%にあたる1168行をランダムに抽出して*学習用データとし、残り全てを精度評価用のデータとしました。なお、新たに特徴量は作成せずすべての列を使って予測しました。
* sklearnのtrain_test_splitを用いて分割した。random_stateは8。
各変数の意味についてはコンペのデータ説明(Data fields)を参照してください。
- MSZoning:5
- Street:2
- LotShape:4
- LandContour:4
- Utilities:2
- LotConfig:5
- LandSlope:3
- Neighborhood:25
- Condition1:9
- Condition2:8
- BldgType:5
- HouseStyle:8
- RoofStyle:6
- RoofMatl:8
- Exterior1st:15
- Exterior2nd:16
- ExterQual:4
- ExterCond:5
- Foundation:6
- Heating:6
- HeatingQC:5
- CentralAir:2
- KitchenQual:4
- Functional:7
- PavedDrive:3
- SaleType:9
- SaleCondition:6
目的変数は対数に変換し、精度評価も対数のまま行いました。
Python(3.7.13)を使用。利用したライブラリのバージョンは下のとおり。
- pandas 1.3.5
- numpy 1.21.6
- sklearn 1.0.2
- lightgbm 2.2.3
結果
評価指標は、コンペ同様にRMSE(二乗平均平方根誤差)としました。
$$\text{RMSE}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(\hat{y_i}-y_i)^2}$$
| LabelEncoder | sort by target mean | sort by target median | sort by count | one-hot encoding | |
|---|---|---|---|---|---|
| linear | 0.146089 | 0.133684 | 0.134490 | 0.144021 | 0.139585 |
| random forest | 0.136293 | 0.135476 | 0.136929 | 0.137594 | 0.138539 |
| LightGBM | 0.124577 | 0.122058 | 0.122089 | 0.123440 | 0.126207 |
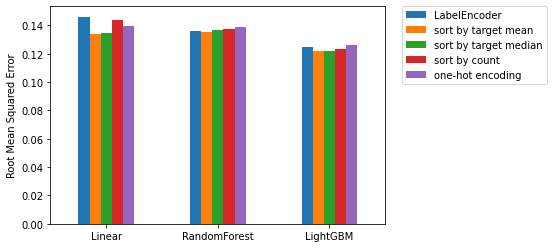
参考までに、最大絶対値誤差と最小絶対値誤差による比較です。
*最大絶対値誤差=\(\displaystyle\max_{i}|\hat{y_i}-y_i|\)
*最小絶対値誤差=\(\displaystyle\min_{i}|\hat{y_i}-y_i|\)
| LabelEncoder | sort by target mean | sort by target median | sort by count | one-hot encoding | |
|---|---|---|---|---|---|
| linear | 1.478429 | 1.320657 | 1.337585 | 1.485624 | 1.542538 |
| random forest | 1.089650 | 1.029509 | 1.033825 | 1.091992 | 1.133581 |
| LightGBM | 0.982768 | 0.864635 | 0.878998 | 0.903554 | 0.930022 |
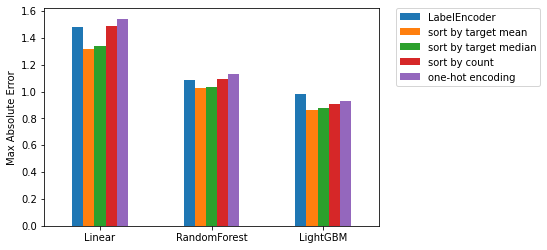
| LabelEncoder | sort by target mean | sort by target median | sort by count | one-hot encoding | |
|---|---|---|---|---|---|
| linear | 0.000484 | 0.000054 | 0.002307 | 0.000170 | 0.000008 |
| random forest | 0.000372 | 0.000038 | 0.000181 | 0.000219 | 0.000177 |
| LightGBM | 0.001111 | 0.000018 | 0.000046 | 0.000092 | 0.000494 |
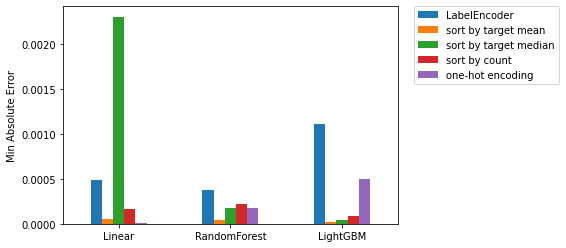
考察
線形回帰モデルは決定木モデルに比べ、数値の割り当て方法による精度のばらつきが大きくなりました。
| RMSEのばらつき(標準偏差) | |
|---|---|
| linear | 0.005540 |
| random forest | 0.001177 |
| LightGBM | 0.001761 |
これは「label encodingが適さない機械学習モデル」の節でも述べましたが、整数値の割り当てかたに何らかの意味(大小関係など)がある場合には、線形回帰でも有効なencodingとなりえます。
今回の場合、
- 目的変数の平均の昇順に0以上の整数を割り振った場合(sort by target mean)
- 目的変数の中央値の昇順に0以上の整数を割り振った場合(sort by target median)
においては、割り振られた整数値が大きければ大きいほど目的変数が大きくなりやすいという、有効な意味をもつencodingになっているため、線形回帰の中でもよい精度を出せたのだと考えられます。
*別の見方をすると、目的変数の情報をlabel encodingに付したから精度が上がった、と考えることもできます。
一方で、決定木系のモデルである「random forest」「LightGBM」ではencodingの仕方によって精度はほぼ変わっていませんね。
まとめ
まとめると、
- 線形回帰系のモデルを使う際には、Encodingの方法を吟味すべし。
- 決定木系のモデルでは、Encoding方法を変えてもあまり意味がない。
- 1つの方法として「目的変数の平均値に基づくlabel encoding」が有効である。
ただし、用いるデータ等によっていろいろ変わってくると思うので、あらゆる場合にあてはまるわけではないことに注意してください。
参考文献
[1] 門脇大輔,阪田隆司,保坂桂佑,平松雄司:Kaggleで勝つデータ分析の技術,技術評論社(2019),p139.
[2]「カテゴリカル変数はなんでもダミー変換すればよいのか?-アルゴリズムに応じたOne Hot EncodingとLabel Encodingの使い分け」キヨシの命題(2018-12-23)
https://yolo-kiyoshi.com/2018/12/23/post-1016/






記事への意見・感想はコチラ