
数学でいきなり相乗平均が出てきたけど、アレいつ使うの…?
って、ふと疑問に思ったことありませんか?
何の前触れもなくいきなり「相加平均・相乗平均の大小関係は…」なんて出てきたので、僕も最初「??」と思いました。
というわけで今回は、相乗平均(別名:幾何平均)の使いどころについて解説していきます。
まずは結論から
結論から言うと、相乗平均は主に「変化率の平均」を求めるときに使います。
「変化率」というのを具体的に挙げてみると下のようになります。
- 経済成長率
- 利益の伸び率
- 投資の利回り
もちろん、上のような経済・金融分野じゃなくても使えます。
「身長が平均○○%伸びた」
「貯金が平均○○%増えた」
など、いろいろと使えます。
その他、「平均収入の平均にも使えるよー」みたいなことをネットで見つけたので、それについてもすこし解説していきます。
なぜ、変化率には相乗平均を使うのか
相加平均で計算してしまうと…。
例として、模試の偏差値で考えてみましょう。
| 回 | 1 | 2 | 3 | 4 |
| 偏差値 | 50.0 | 55.0 | 66.0 | 62.7 |
| 前回比 | 1.10 | 1.20 | 0.95 |
ここで、相加平均で変化率を計算してみましょう。
(1.10+1.20+1.95)÷3 = 1.08333...
となります。
つまり、この4回で模試の偏差値は平均1.08333…倍ずつ伸びていることになります。
しかし!これでは計算が合いません。
平均1.08333…倍ずつになっているということは、
2回目の偏差値=50.0 × 1.0833… = 54.166…
3回目の偏差値=54.166… × 1.0833… = 58.68055…
4回目の偏差値=58.68055… × 1.0833… = 63.570… (??)
となるはずですが、これは実際のデータとは合いません。
ってことは、変化率に相加平均を適用したのは不適切だったということになります。
じゃあ、どう計算すればつじつまが合うのか
では、実際のデータと合うように平均を求めるためにはどうすればいいのでしょうか。
これは、定義に合うように計算すればすぐ出てきます。
**導出過程のようにゴニョゴニョっと計算して、筋が通るようにしたのが、あの相乗平均なんです。
テキトーに
「掛け合わせてルート被せとけばええやろ!」
ってなったわけではありませんよ。
ということで、この相乗平均をつかって再度計算して確かめてみましょう。
| 回 | 1 | 2 | 3 | 4 |
| 偏差値 | 50.0 | 55.0 | 66.0 | 62.7 |
| 前回比 | 1.10 | 1.20 | 0.95 |
1.10 × 1.20 × 0.95 = 1.254
1.254の立方根(3乗根) = 1.078…
となり、この4回で模試の偏差値は平均1.078…倍ずつ伸びていることになります。
ということは、
2回目の偏差値=50.0 × 1.078… = 53.918…
3回目の偏差値=53.918… × 1.078 … = 58.144…
4回目の偏差値=58.144… × 1.078… = 62.7(ピッタリ)
となり、ちゃんと実際のデータとつじつまがあっています。
まとめると「相乗平均 r 」とは
「前回との比率が常に r だとすると、最後(4回目)の偏差値が62.7になる」
ような値のこと、ということになります。
平均所得は、相乗平均で求めるといいらしい
Wikipediaに、こんなことが書いてありました。
例えば、国民(例えば日本人)の所得について考える。このデータでは、一部の高所得者が算術平均値を引き上げてしまい、算術平均値をとる世帯は実際にはほとんどいないということになる。よってこの場合正規分布には従わない。 [中略] 従って、一般的な世帯の所得をとらえるには中央値や最頻値が有効であるが、所得は97%~99%は所得の対数値が正規分布(対数正規分布)に従っているため、所得の対数値の算術平均、つまり幾何平均を用いるのが適切な所得の代表値であるともいえる。
「平均」『フリー百科事典 ウィキペディア日本語版』。2021年8月6日 (金) 10:09 (UTC),URL:https://ja.wikipedia.org/wiki/%E5%B9%B3%E5%9D%87
へぇ~。では実際に、日本の所得の分布を見てみましょう。(厚生労働省による国民生活基礎調査)
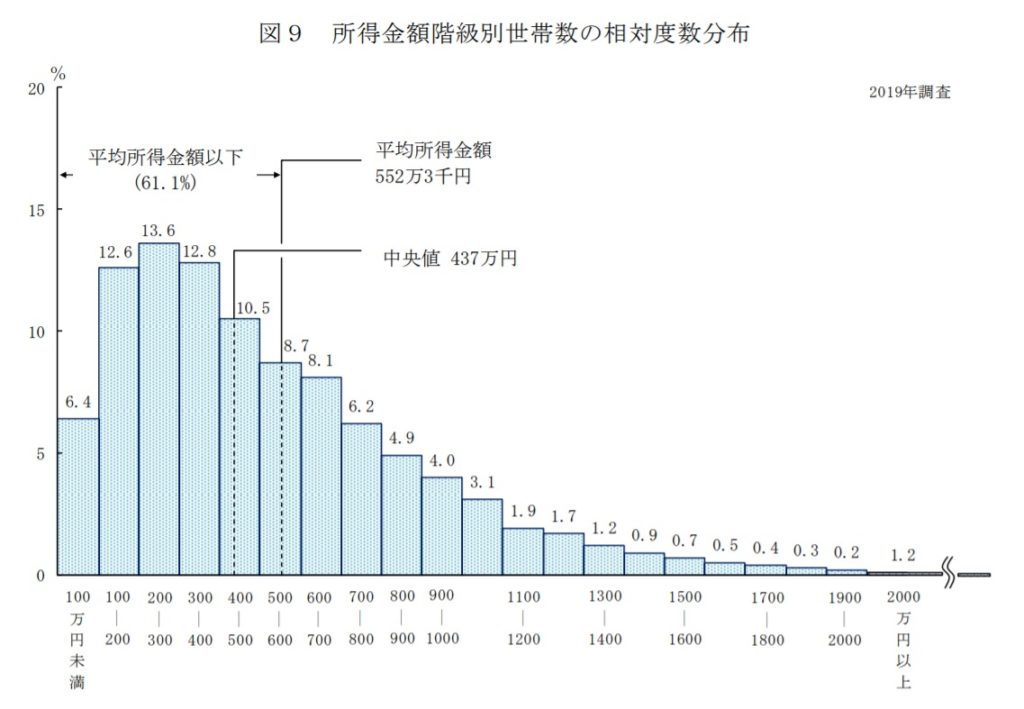
やはり正規分布には従っていなさそうですね…。
なので、普通の相加平均を使うのはあまり適切ではありません。
しかし「幾何平均(=相乗平均)をとればいい感じになるよー」ということなので、とりあえず幾何平均を計算してみました。
結果 …… 385万円 (*グラフの情報から計算したので、おおよその値。)
となりました。
たしかに、
「平均年収552万!」
よりも
「平均年収385万!」
のほうが多くの人にしっくりきそうな感じがします。
ちなみに「なぜ幾何平均をとるのがいいのか?」については補足として簡単に説明しました。(でも…分かりづらいので別に見なくてOK)
まとめ
相乗平均の主な使い道は「変化率」。
変化率じゃなくても、logをとった値が正規分布に従うときには、幾何平均が使える。例えば「平均年収」とか。
*導出過程
「相乗平均がrである」ことの定義は「常にrの比で推移していくと、最後の値に一致する」ことだ、という考えに基づきます。

*補足
まず正規分布というのは、下の図のような形をしています。
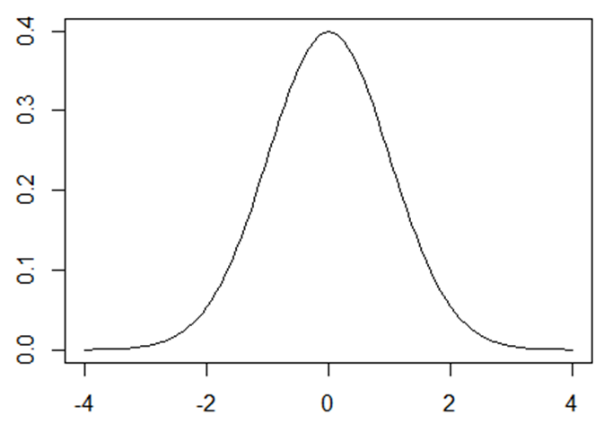
このような形をなすデータの相加平均をとると、山の中央(上図でいうと0)が平均値になります。
しかし日本の所得のように、山が左右どちらか一方に偏っている場合もあります。その場合は、相加平均をとっても山の中央になるとは限りません。
でも、中にはlogをとると正規分布の形に変身するようなデータもあります。日本の所得もその一例でしたね。(正規分布よりは若干ゆがみますが)
そこで、下のような関係に注目します。
相乗平均と相加平均の関係です。
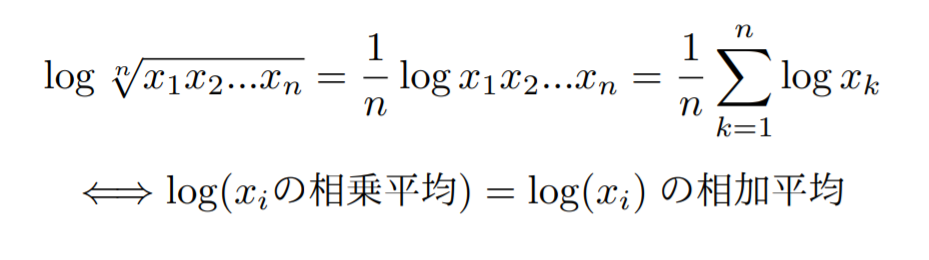
少しややこしくなりますが、続けます。
先ほど「正規分布の相加平均は、山の中央」という話をしました。
同様に、「logをとると正規分布」になるデータでは「logの相加平均」は山の中央になります。
…ということは、「logの相加平均」はデータの特徴を表すのに適切な値ということになります。
よって、上であげた「相乗平均と相加平均の関係」の関係から「相乗平均を使えばいい感じの値になりそうだよねー」とわかります。









記事への意見・感想はコチラ