
こういうデータがあって…
というふうに、客観的なデータをもとに考えるのはとても大事なことです。
そして、データはグラフ化して「見える化」すればわかりやすく伝えることができます。
しかし中には「大げさに見えるように工作しているグラフ」もあったりします。
こういうグラフに騙されない「統計リテラシー」をこの記事で身につけましょう!
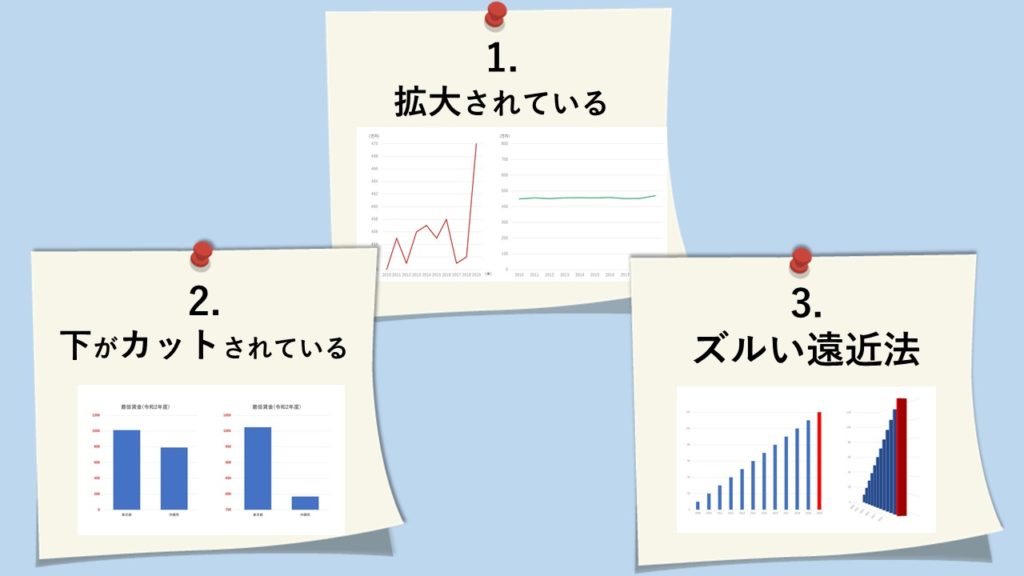
- ”差”をデカく見せるマジック
- グラフを縦に伸ばす
- グラフの下をカット
- ズルい遠近法
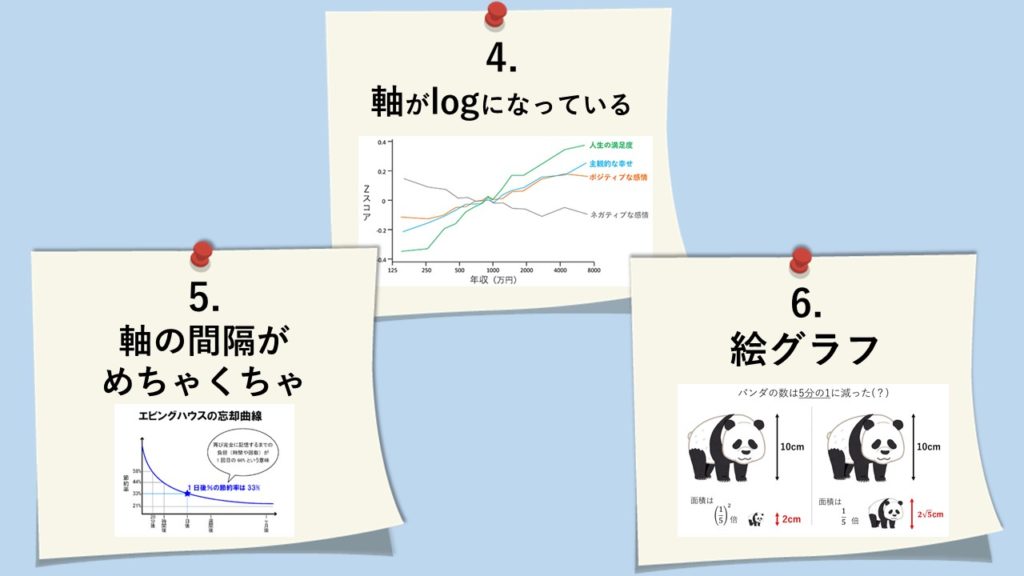
- 数字の”変化”をゆがめるマジック
- 軸を”log”にする
- あのエビングハウスの忘却曲線も…!
- 数字を”誇張”するマジック
- 「高さ」を5分の1倍にしてごまかす
”差”をデカく見せるマジック
グラフを縦に伸ばす
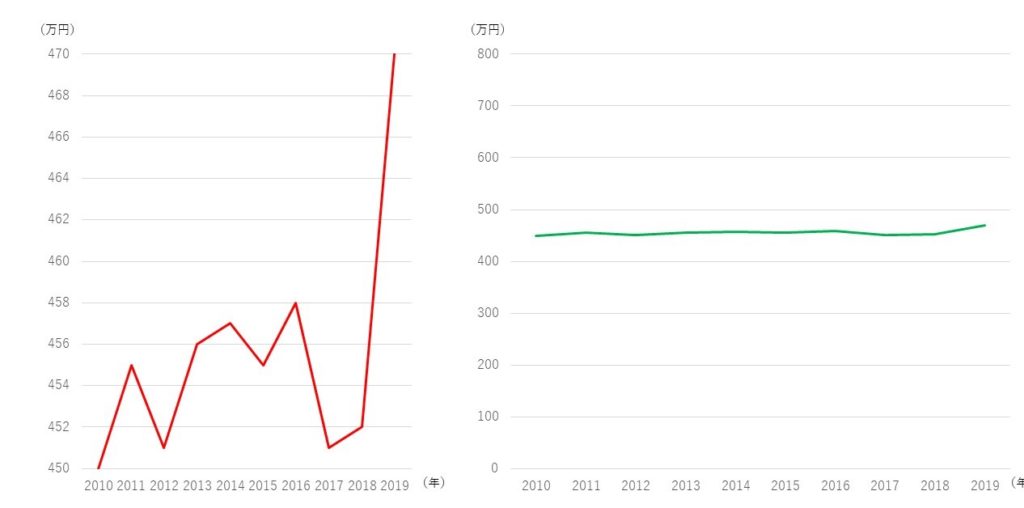
この2つのグラフを見てください。
左:変化が激しく、2019年には激増している?
右:変化はあまりなく、安定的
といった印象を持つと思います。
しかし実はこの2つのグラフ、
同じデータをもとに作られています。
なぜこんなにも違うグラフになったのでしょう?
そのタネは、
左グラフの縦軸:450~470万円
右グラフの縦軸:0~800万円
となっていることです。
つまり、左のグラフでは
変化が大きく見えるように拡大しているのです。
たったこれだけで、イメージを操作できてしまいます。

2019年、給料がバーンと跳ね上がりましたよ…!
と言いたければ左のグラフを使いたくなるし、

この会社の給料は安定していますよ!
と言いたいなら右のグラフを使うでしょう。
このようなグラフで振り回されないためには、
✓縦軸はどうなっている?
✓グラフで見せられた”差”や”変化”はそれほど重要か?
といったことの確認を怠らないことです。
グラフの下をカット
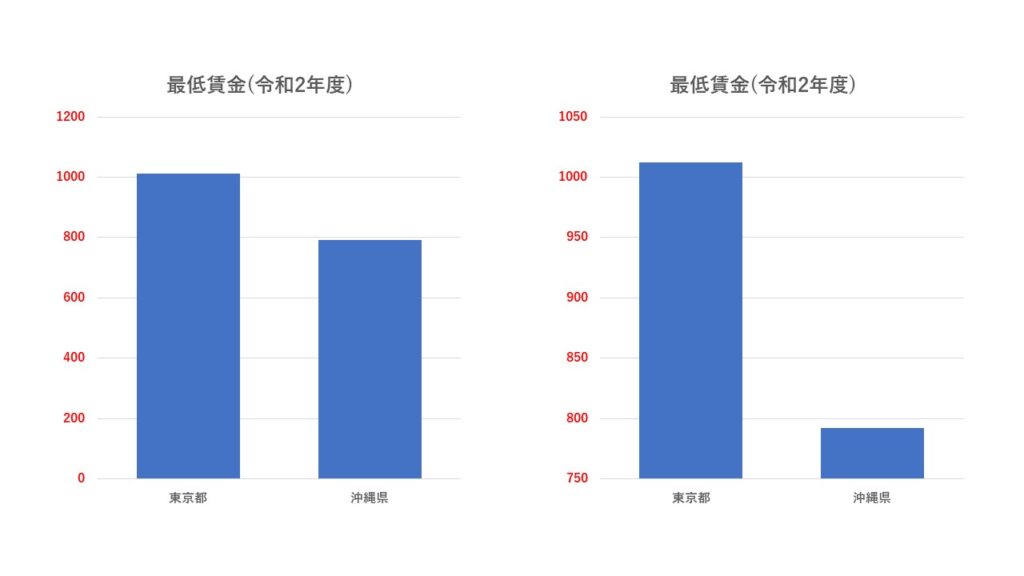
こちら2つのグラフも、
同じデータをもとに作られたものですが、
印象が全く違いますよね。
右のグラフを出されると、

地方格差、デカすぎる…!
というイメージが強くなります。
これはなぜかと言ったら、
棒グラフの下がカットされている
からです。
たったこれだけで、東京都と沖縄県の差を
デカく見せつけることができてしまいます。
このようなグラフで振り回されないためには
先ほどと同様、
✓縦軸はどうなっている?
✓グラフで見せられた”差”や”変化”はそれほど重要か?
といったことの確認をすることが重要です。
ズルい遠近法
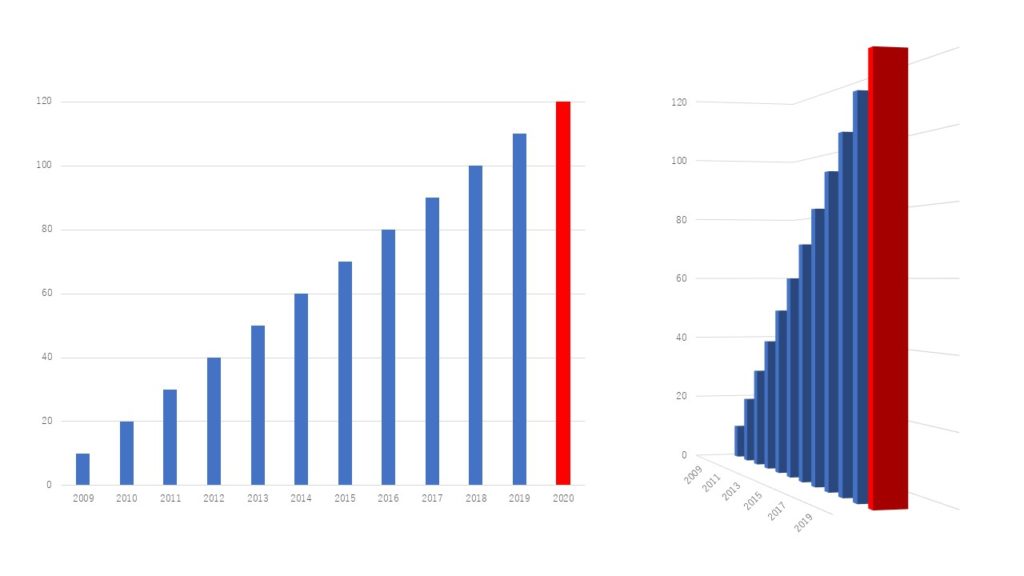
こちらは「A塾の合格者数」を表したものになります。
(架空のデータです)
右のグラフは、左のグラフを3D化し
斜めから見たものです。
すると、どうでしょう。
右のグラフのほうが、
「圧倒的合格者数!」
という感じが出ませんか?
このトリックとしては、
遠くにあるものは余計に小さく見え、
近くにあるものは余計に大きく見える。
というものです。
まさに「ズルい遠近法」です。
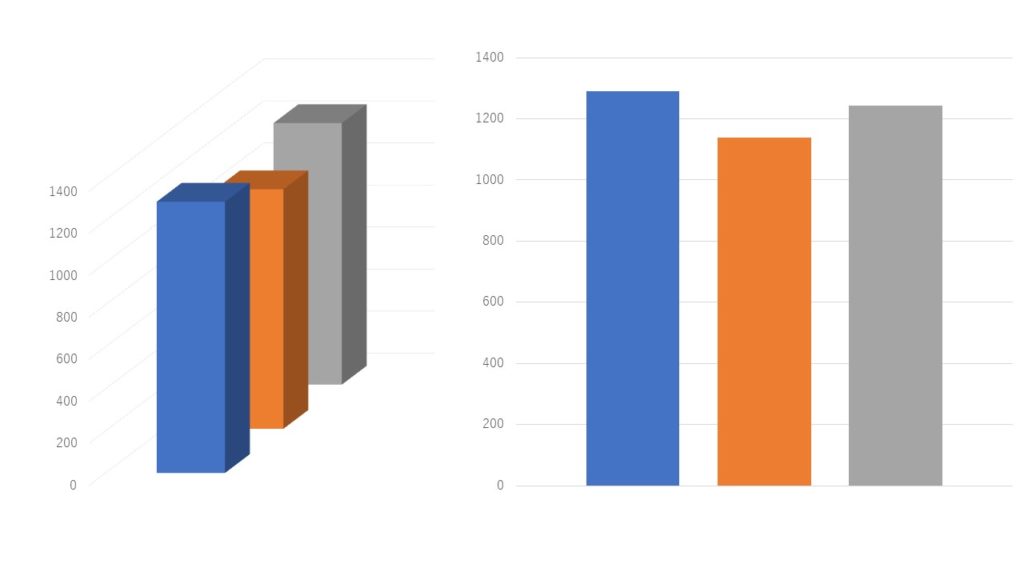
今度は、こちらの3Dグラフを見てみましょう。
3Dグラフで見ると、

グレー>青>オレンジ
の順に多いかな…?
と思う方が多いと思います。
しかし…。
右のグラフは、3Dではなく平面にしたもので、
それを見ればわかる通り、実は
「青>グレー>オレンジ」の順に多いです。
上の2つの例のように、
立体的なグラフは誤解を招くことが多いので、
特に注意して見なければいけません。
なので3Dグラフを見たら、
何か誇張していないか?
大小関係がごまかされていないか?
を確認しましょう。
数字の”変化”をゆがめるマジック
軸を”log”にする
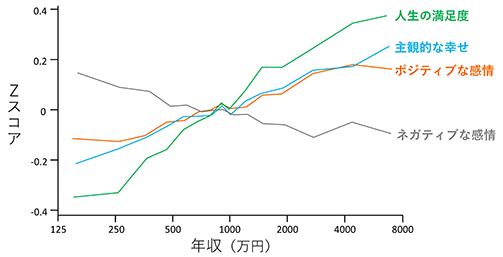
このグラフを見て、

「Zスコア」と「年収」は
直線的な関係にあるんだな…!
と判断してしまった人、残念…!
このグラフの横軸をよ~く見てください。
125→250→500→1000→2000→4000→8000
と2倍になっています(公比が2の等比数列)。
目盛りが等間隔になっていない!
しかし、ある見方をすると”等間隔”になっています。
2を底とする対数をとってみると、
log2125→log2250→log2500→log21000
→log22000→log24000→log28000
ここで、対数の性質
log2ab = log2a + log2b
を使うと、
log2125→log2125+1→log2125+2→log2125+3
→log2125+4→log2125+5→log2125+6
となって、1ずつ増えています。
つまり、対数(log)をとることで
等間隔でないものを等間隔にできてしまうのです。
だから、さっきの男の子の考えを修正するとすれば、

「Zスコア」と「年収の対数」は
直線的関係にあるんだな…!
ということになります。
よ~く見ないとまんまと騙されてしまいます。
軸の目盛りは等間隔か?
ということをしっかり確認しましょう。
あのエビングハウスの忘却曲線も…!
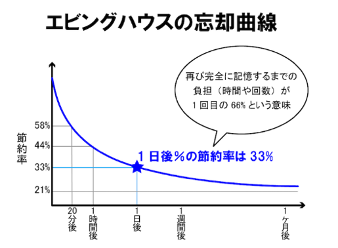
こちらのグラフは、
受験を経験した人なら1度は耳にする
「エビングハウスの忘却曲線」です。
ですが、冷静に見てください。
横軸の間隔がおかしい!
しかも対数ではなさそう…。
世に出回っている忘却曲線は、
だいたいこんな形をしています。
きれいなグラフにしたいからなのか分かりませんが、
世に出回っている忘却曲線のほとんどが「横軸の間隔がおかしい」です。
ということで、横軸の間隔を正しくしたものを作りました。
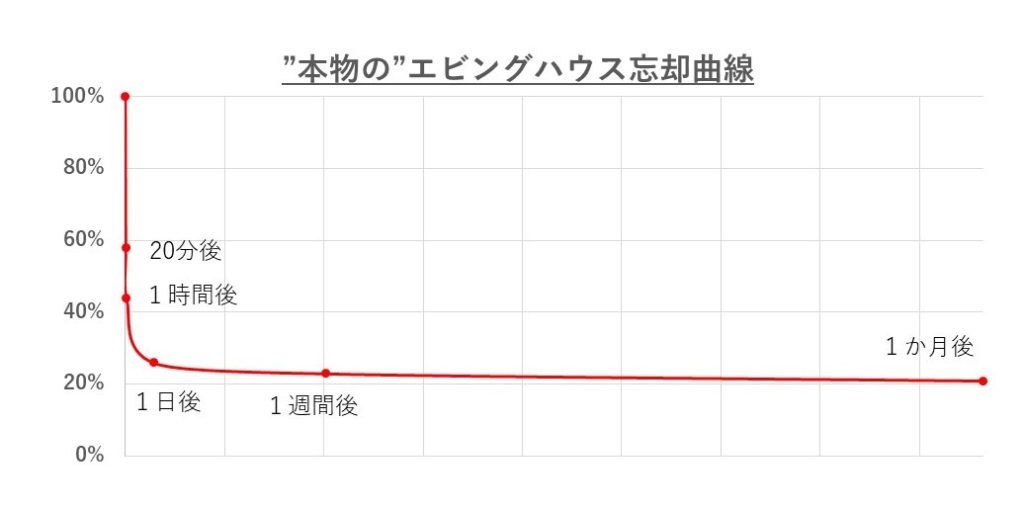
こうすれば、受験アドバイスによくある

エビングハウスの忘却曲線によれば、
学習直後にもっとも早く忘れてしまうので…
という主張も、この正しいグラフを出せば大いに納得できるでしょう。
なのにわざわざ、緩やかなグラフを持ち出して説明しているのです。
僕にとっては不思議でなりません…。
数字を”誇張”するマジック
「高さ」を5分の1倍にしてごまかす
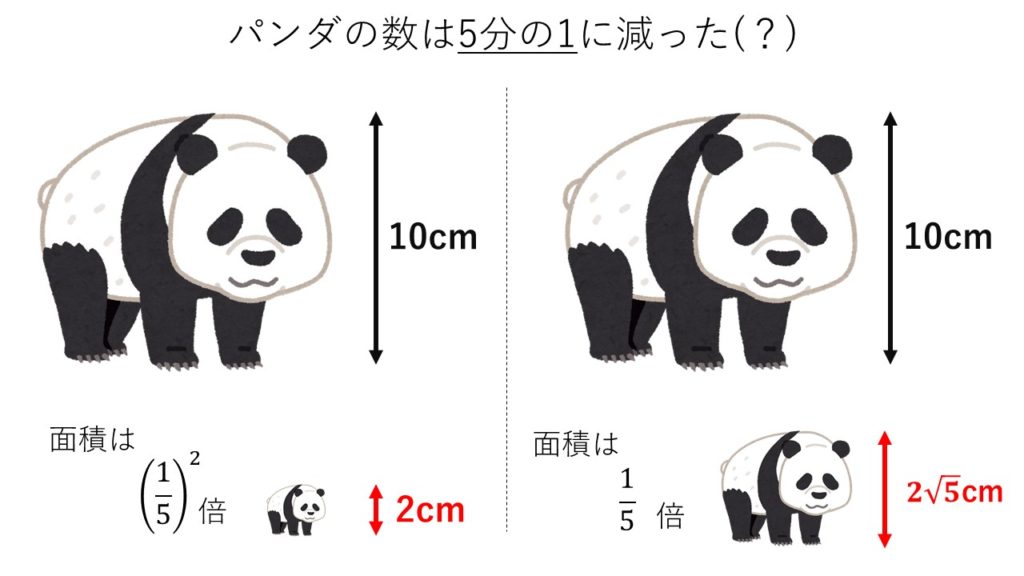
今度は「パンダの数が5分の1になった」
ということを「絵」で表現します。
そのためには、パンダの画像と、
その面積を5分の1にした画像を用意すれば良さそうですよね。
(立体的な効果を考慮して、見かけの体積を5分の1にしたほうが良い場合もある)
ところが、

よし、画像の高さを5分の1にすればOK!
と考えてしまう人がたまにいます。
長方形の辺の長さをA倍にすると面積はA2倍になります。
なので、画像の面積は25分の1となってしまい
「パンダの数が激減した!」というイメージが
誇張されてしまいます。
(それが良いか悪いかは別問題ですが)
よって、画像の縦横の長さは√5分の1にしなければならないはずです。
さっきの少年のように、
単純にミスしてしまっただけの場合もありますが、

ほら、高さが5分の1になっているでしょ!
といいながら、意図的にやっている場合もあるので注意が必要です。
イメージ図に振り回されることなく、
数字で状況を判断しよう。
今回のまとめ








記事への意見・感想はコチラ