
対数って何の役に立つの?
本記事ではこの悩みに答えていきます。
まず、対数(log)の使い道を最初にまとめておきます。
- 身近な単位に使われている
- マグニチュードと震度
- 酸塩基性をはかる「pH」
- 音の大きさ「デシベル」
- 星の明るさ「等級」
- 計算量を削減できる
- 電卓がない時代、計算が楽に
- デカい数字を小さな数で表せる
- 対数軸グラフ
このように、対数は日常生活の中でもよく聞くような単位にも使われています。また、対数はもともと大きな数の計算を楽に行うために考案されたものなので、計算量を削減できるという大きなメリットもあります。
身近な単位に使われている
物理学で扱われる単位の中には、対数をもとにしたものがいくつかあります。その中でも身近なものをご紹介します。
マグニチュードと震度
「マグニチュード」は地震のエネルギーの大きさを表す単位で、「震度」は地震の揺れの強さを表す指標です。なので「マグニチュード」と「震度」はよく混同されますが、本当は全く異なる指標ですから注意してください。
「マグニチュード」は地震のエネルギーを表す単位ですが、地震のエネルギーはものすごくデカいです。例えば東日本大震災の地震のエネルギーは約2,000,000,000,000,000,000(=2×1018)ジュールです。こんな莫大な数字を地震が起こるたびに毎回扱っていては大変です。
そこで、対数をとることを考えてみます。東日本大震災の地震のエネルギーを常用対数で表してみると、log10(2×1018) ≒ 18.3 となります。かなり扱いやすい数字になりますよね。
しかしただ単に対数を取っただけでは、ふだん私たちが目にする「マグニチュード」の値にはなりません。地震のエネルギーをE,マグニチュードをMとすると次の式が成り立ちます。
$$\log_{10}E = 4.8 + 1.5M$$
これでマグニチュードの計算ができます。
酸塩基性をはかる「pH」
pH [水素イオン指数] とは、溶液がどれくらい酸性あるいは塩基(アルカリ)性なのかを表す指標です。ちなみに、pHという記号はラテン語の「pounds Hydrogenii」から来ています。
pHの計算は高校化学でも計算問題でよく登場します。pHは水素イオン濃度の逆数の常用対数です。すなわち
$$pH = -\log_{10}[H^+]$$
です。
音の大きさ「デシベル」
騒音の大きさなどを表すときによく「デシベル(dB)」という単位をよく聞きますよね。じつはこの「デシベル」も対数がもとになっています。
理科でも習うように、音の正体は空気の振動です。空気が密になっている(=音圧が大きい)ほど、音は大きく聞こえます。しかし、音圧が2倍になれば人間にとっての音の大きさも2倍になるかというと、実はそうではありません。
例えば「1gと100gの違い」はすぐに分かりますが「10.001kgと10.1kgの違い」はなかなかわかりません。同じ99gの差であるにもかかわらず、です。
このように人間は大きな刺激を受けるとき、その刺激の違いに気づきづらくなります。これは「ヴェーバー・フェヒナーの法則」として知られていて、人間が感じる刺激の強さEは実際の刺激の強さRを用いて
$$E=C\log R$$
と表されることがわかっています。
人間の聴覚もこの法則にしたがうので、騒音の大きさを表すデシベルも音圧の対数を取って求められます。(実際は単に対数を取るだけではない)
星の明るさ「等級」
人間が感じる「光の強さ」も先述のウェーバー・フェヒナーの法則にしたがいます。
等級\(m\)は,天体の明るさ\(l\)とゼロ等級の明るさ\(l_0\)を用いて
$$m=-2.5 \log_{10}\frac{l}{l_0}$$
と表されます。
計算量を削減できる
電卓がない時代に大活躍
対数は、ジョン・ネイピアという人によって1594年ごろに考案されました。
ネイピアの生きた時代は大航海時代でした。海を越えた旅をするには天文学を駆使した計算が必要です。しかしその計算をするには面倒な三角関数の計算をしなければなりません。当時は電卓などないので手計算に頼るほかありませんでした。
そこでネイピアは、頭を抱えて計算に苦しむ天文学者を助けるべく、新しい計算方法を見つけ出そうと決意したのです。
そして1594年に対数の概念に到達し、その後20年かけて「対数表」を完成させました。

しかしこの対数表は0.9999999という微妙な数を底としており、人々にはあまり理解されませんでした。しかしのちに、ヘンリー・ブリッグスという天文学者によって「10を底とする対数」が考案され、これが世界中に知れ渡ることになりました。
では、なぜ対数をつかうと計算が楽になるのでしょうか?
一番大きいのは「積」を「和」で表せるということです。
たとえば、123 × 456 × 789 × 135 × 792 をまともに計算しようと思ったらかなり大変です。そこで常用対数をとったものを計算しておいて、最後に戻すことにしてみましょう。すると
$$\begin{align*}
\log_{10}(123\times456\times789\times135\times792) &=
\log_{10}(1.23\times4.56\times7.89\times1.35\times7.92\times10^{10}) \\
&=\log_{10}1.23 + \log_{10}4.56 + \log_{10}7.89 + \log_{10}1.35 + \log_{10}7.92 + 10 \\
&= 0.0899 + 0.6590 + 0.8971 + 0.1303 + 0.8987 + 10\\
&= 12.675\\
\therefore 123\times456\times789\times135\times792 &= 4.73\times10^{12}
\end{align*}$$
となります(常用対数表しか使っていない)。正確な答えは4,731,576,949,440 ≒ 4.73×1012なので、おおむねあっています。
この計算の最大のポイントは、上式の1行目から2行目の変形です。面倒なかけ算が足し算に置き換わっています。そのおかげで計算量が大幅に削減できているのです。
現代でも対数は有用
しかし、現在は電卓があるので対数なんかを使わなくても一瞬で計算できてしまいます。
じゃあ対数は必要ないのか、というとそうではありません。
コンピューターにも扱える情報量に限界があります。なので、11482447354256431544の24316146乗を計算しろ!と言っても数がデカすぎて扱いきれません。しかし対数をとることで、処理能力の範囲内に収めることができます。
たとえば、100000000000000000000という値はダメでも、常用対数をとると 20 になるので余裕で扱えます。
機械学習、とくにニューラルネットワークと呼ばれる分野の計算過程では非常に大きな数を扱う必要が出てきます。そのときに限界をこえた数になってしまうと思わぬ結果が出てしまうので、対数を駆使することでそれを防いでいます。
対数軸グラフ
最後は対数軸グラフです。下のグラフを見てください。
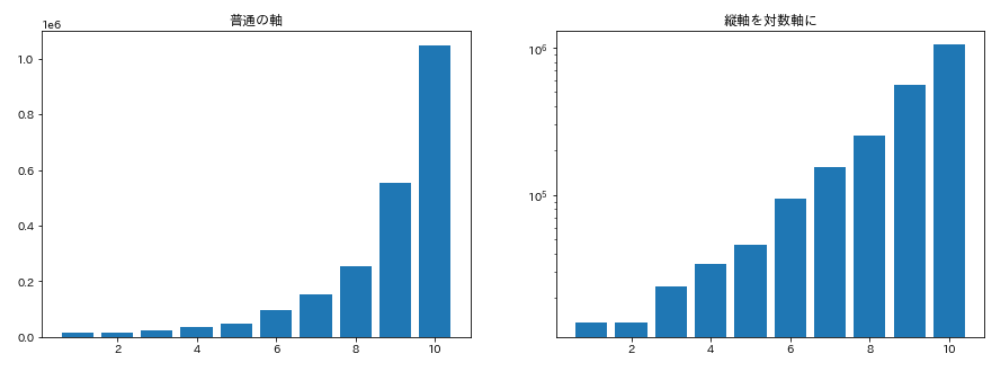
左のグラフは普通に描いた棒グラフです。高い棒があるせいで、左のほうにある低い棒たちはほとんど同じ高さに見えてしまいます。これでは、小さな数どうしを比較するのが難しいです。
そこで右のグラフのように、縦軸を「対数スケール」にしてみます。
「対数スケール」にするとは、通常は「1,2,3,4,5,…」となる軸を「log1,log2,log3,log4,log5,…」のように対数をとることをいいます。
このように軸を対数にすると、小さな数から大きな数まで差がきちんと見えるようにすることができます。グラフが見にくくなったときには、このような対数変換が有効になります。
なお、「これは対数軸です」などと断っておかないと誤解を招くことになるので、きちんと注釈はつけておくようにしましょう。





記事への意見・感想はコチラ
地震の対数が違うと思う。
18.3だと思う。
確認願います。
ご指摘ありがとうございます!
おっしゃるとおり、エネルギーの常用対数をとった値が間違っておりました。
× 5.4
○ 18.3
お詫びして訂正いたします。
間違えました。名前の欄に。